Inner product matrix

Note that the outer product is defined for different dimensions, while the inner product requires the same dimension. If the dimensions are the same. In mathematics, the Frobenius inner product is a binary operation that takes two matrices and returns a number. The operation is a component-wise inner product of two matrices as though they are vectors.

The two matrices must have the same dimension—same number of rows and columns—but are not restricted to be square matrices. An inner product is a generalization of the dot product. In a vector space, it is a way to multiply vectors together, with the result of this multiplication being a scalar. Let u, v, and w be vectors and alpha be a scalar, then: 1. It is valid problem since it meets the matrix inner product rule as shown below.

The calculation is as simple as follows. Vector inner product is also called vector scalar product because the result of the vector multiplication is a scalar. It can only be performed for two vectors of the same size.

Geometrically, vector inner product measures the cosine angle between the two input vectors. Inner product of two arrays. Parameters a, b array_like.

If a and b are nonscalar, their last dimensions must match. Returns out ndarray. The concept of an inner product is one of the most important matrix algebra concepts, also commonly referred to as the dot product.

The standard Dot product in Mathematica does not properly handle the inner product of vectors whose components are operators, because it tries to contract the last index of the first argument with the first index of the second argument. What is the correct definition of the standard inner product of two given matrices ? Stack Exchange Network Stack Exchange network consists of 1QA communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Property of the conjugate transpose matrix with inner product (answer) Closed years ago. If you want to perform all kinds of array operations, not linear algebra, see the next page. Multiplies two matrices, if they are conformable.

If one argument is a vector, it will be promoted to either a row or column matrix to make the two arguments conformable. If both are vectors of the same length, it will return the inner product (as a matrix ). The inner product is used all the time the outer product it is not use really used that often but there are some numerical methods, there are some techniques that make use of the outer product. So, as a student and matrix algebra you should know what an outer product is.

The inner product between two vectors was U transpose V for to column vectors that gave us a scalar, but what would happen. Infinity) maximum entry A. The inner product of a vector with dimensions 2x(rows, column) with another vector of dimension 2x(rows, column) is a matrix with dimensions 2x(rows, columns).

This ensures that the inner product of any vector with itself is real and positive definite. Unlike the relation for real vectors, the complex relation is not commutative, so dot(u,v) equals conj(dot(v,u)). The Numpu matmul() function is used to return the matrix product of arrays.

Here is how it works. D arrays, it returns normal product. Tr(Z) is the trace of a real square matrix Z, i. First, we check the dimensions of the matrices.

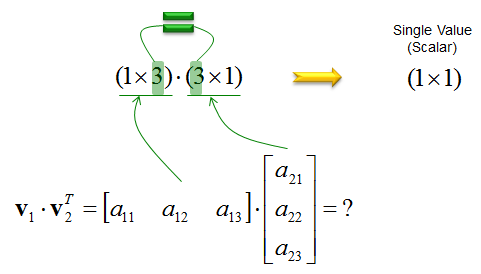
The inner dimensions are the same so we can perform the multiplication. If you transpose V equals zero then we say that two vectors are orthogonal, the norm of the vector which is equivalent to the length of the vector is U transpose U raised to the half power, so square root of the sum of the squares of the components. We say U is normalized if the norm is equal to one, and if we have a set of vectors.

Check the three properties of inner product. Notice that the matrix is not symmetric. This suggests that the function described above might fail the symmetry property of inner products.

Find the matrix of the standard inner product on W (obtained by restriction of the dot product on Rª) with respect to the basis S. Please solve (3), (4), and (5), use typefont, and show your work. Homework Statement: Image attached Relevant Equations.